ЦЕПНЫЕ ДРОБИ
В некоторых приложениях математики встречаются очень громоздкие дроби. Возникает вопрос, нельзя ли подобрать дробь со сравнительно небольшим знаменателем, достаточно близкую к данной громоздкой дроби. Аппаратом для решения этой задачи являются дроби особого вида, называемые цепными или непрерывными дробями.
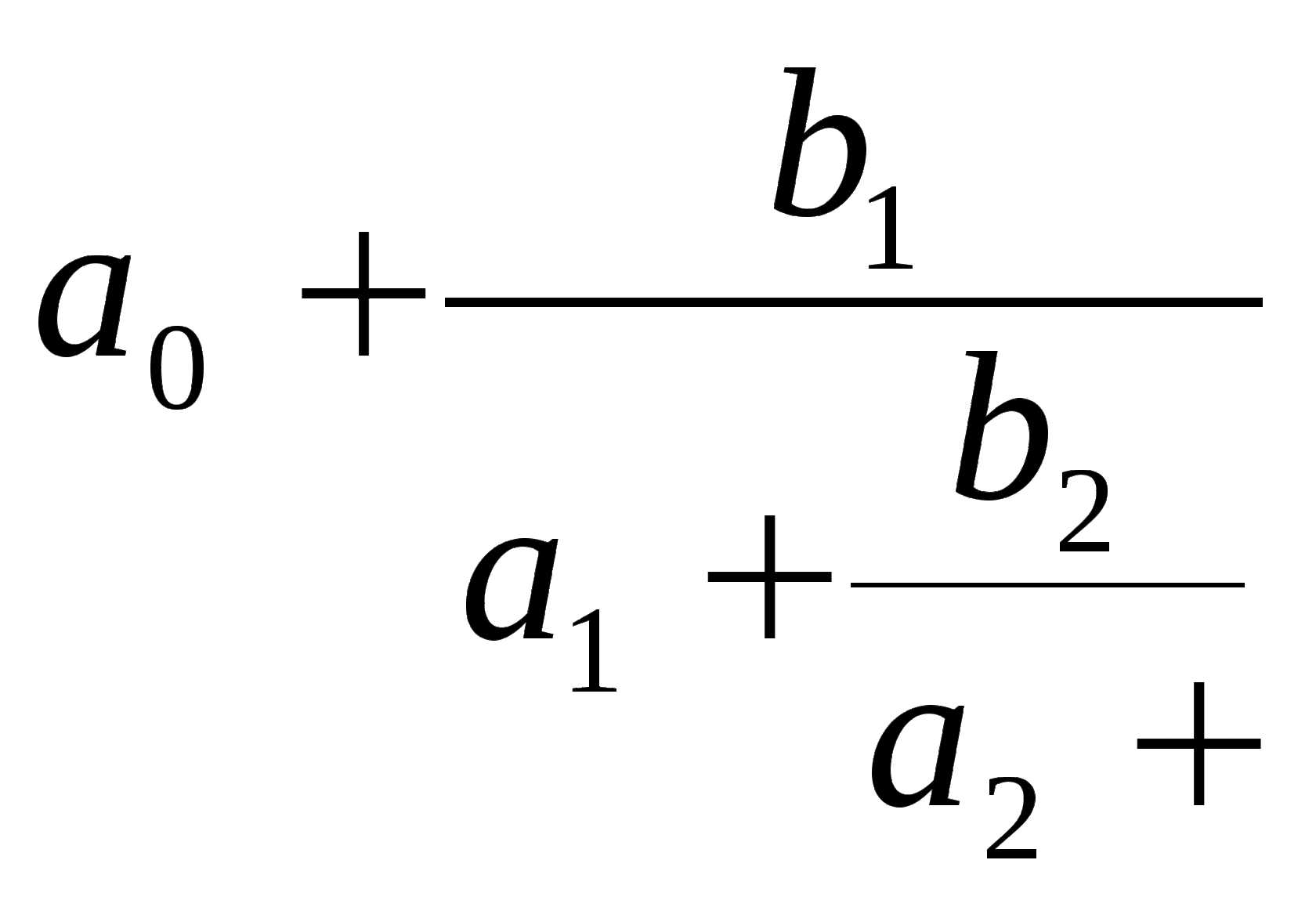
Непрерывная дробь (или цепная дробь) — это конечное или бесконечное математическое выражение вида
Любое вещественное число можно представить в виде цепной дроби (конечной или бесконечной). Число представляется конечной цепной дробью тогда и только тогда, когда оно рационально.
Непрерывные дроби широко используются в теории чисел и вычислительной математике, а их обобщения оказались чрезвычайно полезны в математическом анализе и других разделах математики. Используются также в физике, небесной механике, технике и других прикладных сферах деятельности.
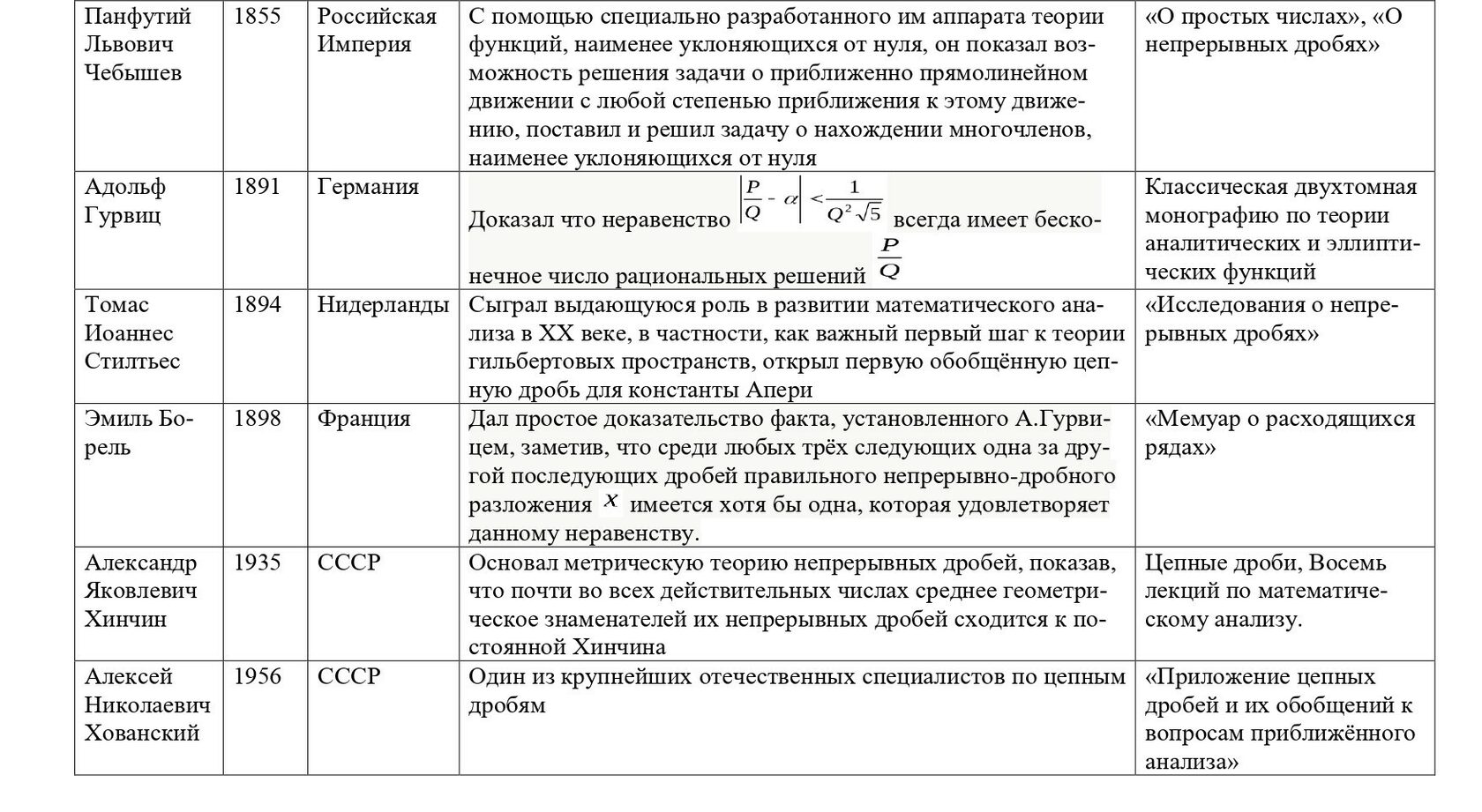
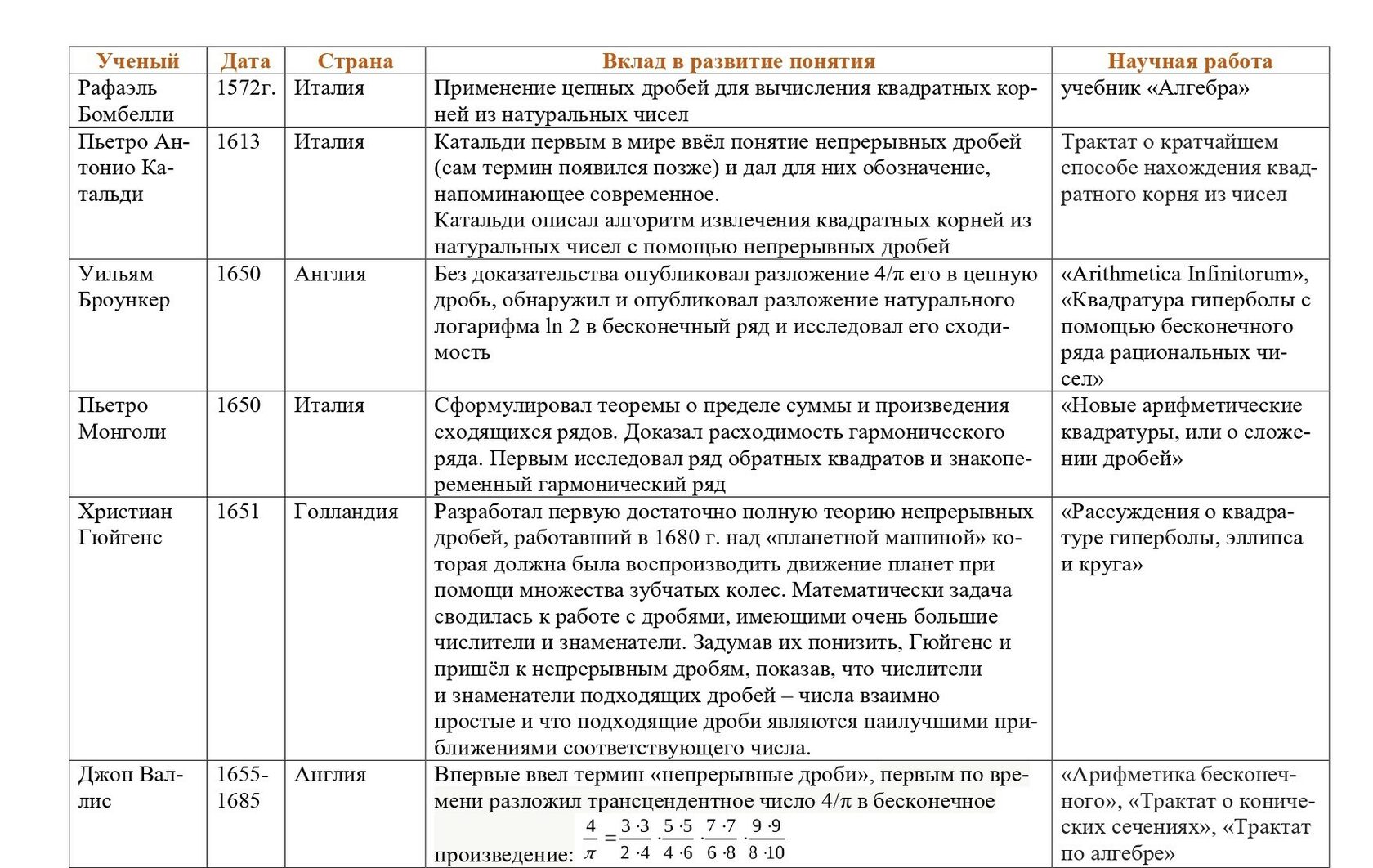
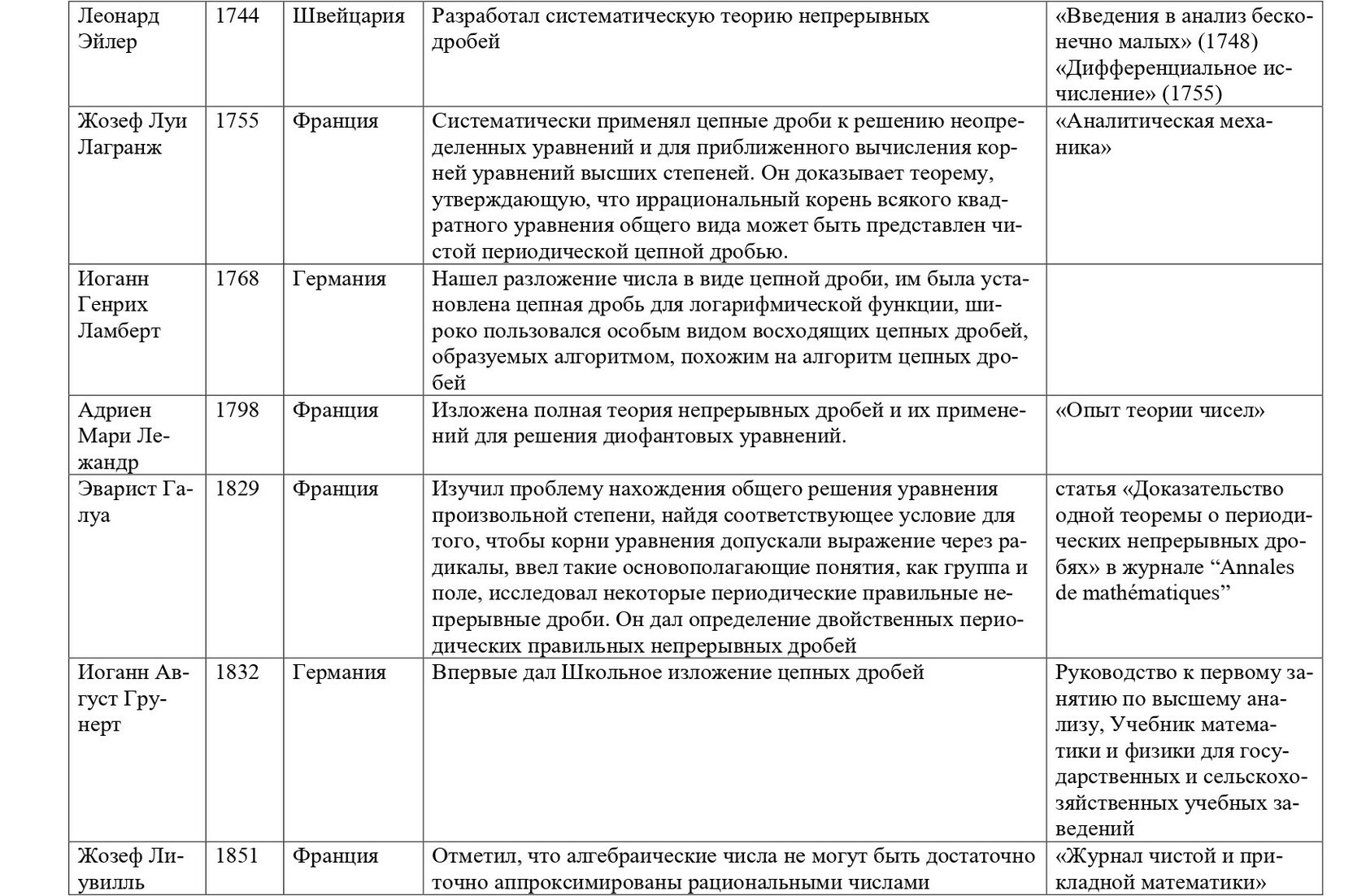
Предлагаем проследить историю развития понятия "цепная дробь" в следующей таблице
Христиан Гюйгенс
(1629-1695гг.)
(1629-1695гг.)

Голландский естествоиспытатель, был одной из величайших фигур научной революции. Хотя его самым известным изобретением являются часы с маятником, Гюйгенса помнят за широкий спектр изобретений и открытий в области физики, математики, астрономии и часового дела. В дополнение к созданию влиятельного устройства для измерения времени, Гюйгенс открыл форму колец Сатурна, спутника Титана, волновую теорию света и формулу центростремительной силы.
Гюйгенс имел тенденцию публиковаться спустя долгое время после совершения своих открытий. Он хотел убедиться, что его работа была правильной, прежде чем представить ее своим коллегам.
Гюйгенс верил, что жизнь может быть возможна на других планетах. В "Космотеоросе" он писал, что ключом к внеземной жизни является наличие воды на других планетах.



Биография Христиана Гюйгенса

В дополнение к самым известным открытиям Гюйгенса, ему приписывают несколько других заметных вкладов:
- Гюйгенс ввел музыкальную шкалу с 31 равным темпераментом, которая связана со шкалой meantone Франсиско де Салинаса.
- В 1680 году Гюйгенс сконструировал двигатель внутреннего сгорания, который использовал порох в качестве топлива. Он так и не построил их.
- Незадолго до своей смерти Гюйгенс завершил "Космотеорос". Она была опубликована посмертно. В дополнение к обсуждению возможности существования жизни на других планетах, он предложил, чтобы ключевым критерием для поиска внеземной жизни было бы наличие воды. Он также предложил метод оценки расстояний между звездами.
Избранные опубликованные работы
- 1651: Циклометрия
- 1656: Новая обсерватория Луны Сатурна (об открытии Титана)
- 1659:Система сатурния (о планете Сатурн)
- 1659: De vi centrifuga (о центробежной силе, опубликовано в 1703)
- 1673: Horologium oscillatorium sive de motu pendularium (дизайн часов с маятником)
- 1684: Astroscopia Compendiaria tubi optici molimine liberata (составные телескопы без трубки)
- 1690: Traité de la lumière (treatise on light)
- 1691:Письмо о циклической гармонике (о 31-тоновой системе)
- 1698: Космотеорос (о космологии и жизни во Вселенной)
Советские ученые, внесшие вклад в изучение цепных дробей



П.Л.Чебышёв (1821-1894) —получил фундаментальные результаты в теории чисел (распределение простых чисел) и теории вероятностей (центральная предельная теорема, закон больших чисел), построил общую теорию ортогональных многочленов, теорию равномерных приближений и многие другие. Основал математическую теорию синтеза механизмов и разработал ряд практически важных концепций механизмов.
А.А.Марков (1856-1922) - награждён золотой медалью за сочинение «Об интегрировании дифференциальных уравнений при помощи непрерывных дробей» защитил свою знаменитую магистерскую диссертацию «О бинарных квадратичных формах положительного определителя», защитил докторскую диссертацию «О некоторых приложениях алгебраических непрерывных дробей».
И.В.Слешинский (1854-1931) - Труды ученого посвящены непрерывным дробям, способу наименьших квадратов, теории вероятностей. В центре внимания Слешинского и его учеников были вопросы, связанные с использованием математической логики к обоснованию математики.



А.Н.Хованский (1916-1996) - одним из ведущих учёных специалистов в области цепных дробей в СССР и за рубежом, опубликовал монографию «Приложение цепных дробей и их обобщений к вопросам приближённого анализа»
Г.В.Маурер (1937-2003) - Научные исследования в области аналитической теории цепных дробей и ее приложению. Автор более 21 научных и учебно-методической работ.
А.Я Хинчин (1894-1959)- создал теорию аппроксимативных производных и обобщил понятие интеграла Данжуа (в узком смысле), придя к более общей конструкции интеграла Данжуа — Хинчина, которая позволяет восстанавливать первообразную функции по её аппроксимативной производной. применил методы метрической теории функций к задачам теории вероятностей и теории чисел. Им получены важные результаты в области предельных теорем, открыт закон повторного логарифма. Одним из значительных результатов является формула Леви — Хинчина для характеристической функции процесса в теории стохастических процессов Леви.